二分搜索怎么用？我又总结了套路

labuladong2022-08-142024-02-15

二分搜索怎么用？我又总结了套路

读完本文，你不仅学会了算法套路，还可以顺便解决如下题目：

LeetCode	力扣	难度
1011. Capacity To Ship Packages Within D Daysopen in new window	1011. 在 D 天内送达包裹的能力open in new window	🟠
410. Split Array Largest Sumopen in new window	410. 分割数组的最大值open in new window	🔴
875. Koko Eating Bananasopen in new window	875. 爱吃香蕉的珂珂open in new window	🟠
-	剑指 Offer II 073. 狒狒吃香蕉open in new window	🟠

我们前文我写了首诗，把二分搜索变成了默写题详细介绍了二分搜索的细节问题，探讨了「搜索一个元素」，「搜索左侧边界」，「搜索右侧边界」这三个情况，教你如何写出正确无 bug 的二分搜索算法。

但是前文总结的二分搜索代码框架仅仅局限于「在有序数组中搜索指定元素」这个基本场景，具体的算法问题没有这么直接，可能你都很难看出这个问题能够用到二分搜索。

所以本文就来总结一套二分搜索算法运用的框架套路，帮你在遇到二分搜索算法相关的实际问题时，能够有条理地思考分析，步步为营，写出答案。

#原始的二分搜索代码

二分搜索的原型就是在「有序数组」中搜索一个元素 target，返回该元素对应的索引。

如果该元素不存在，那可以返回一个什么特殊值，这种细节问题只要微调算法实现就可实现。

还有一个重要的问题，如果「有序数组」中存在多个 target 元素，那么这些元素肯定挨在一起，这里就涉及到算法应该返回最左侧的那个 target 元素的索引还是最右侧的那个 target 元素的索引，也就是所谓的「搜索左侧边界」和「搜索右侧边界」，这个也可以通过微调算法的代码来实现。

我们前文我写了首诗，把二分搜索变成了默写题详细探讨了上述问题，对这块还不清楚的读者建议复习前文，已经搞清楚基本二分搜索算法的读者可以继续看下去。

在具体的算法问题中，常用到的是「搜索左侧边界」和「搜索右侧边界」这两种场景，很少有让你单独「搜索一个元素」。

因为算法题一般都让你求最值，比如让你求吃香蕉的「最小速度」，让你求轮船的「最低运载能力」，求最值的过程，必然是搜索一个边界的过程，所以后面我们就详细分析一下这两种搜索边界的二分算法代码。

注

注意，本文我写的都是左闭右开的二分搜索写法，如果你习惯两端都闭的写法，可以自行改写代码。

「搜索左侧边界」的二分搜索算法的具体代码实现如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

// 搜索左侧边界
int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 当找到 target 时，收缩右侧边界
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left;
}

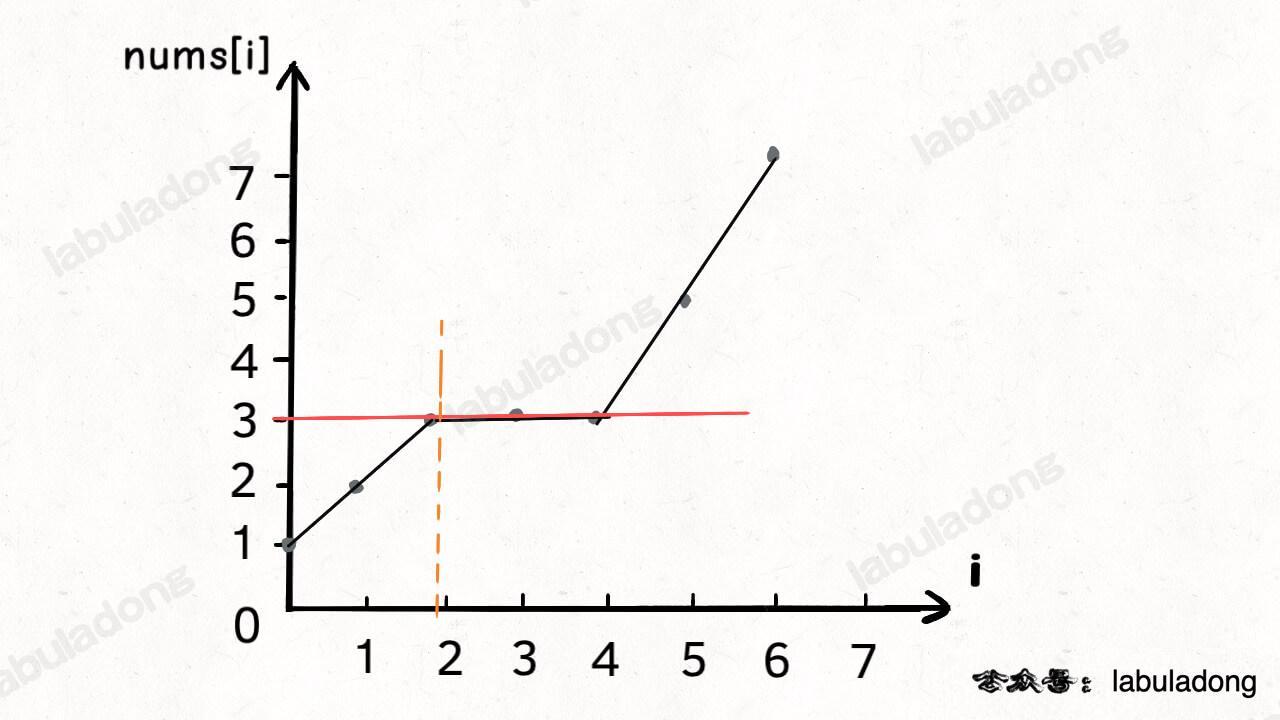
假设输入的数组 nums = [1,2,3,3,3,5,7]，想搜索的元素 target = 3，那么算法就会返回索引 2。

如果画一个图，就是这样：

「搜索右侧边界」的二分搜索算法的具体代码实现如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

// 搜索右侧边界
int right_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 当找到 target 时，收缩左侧边界
            left = mid + 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1;
}

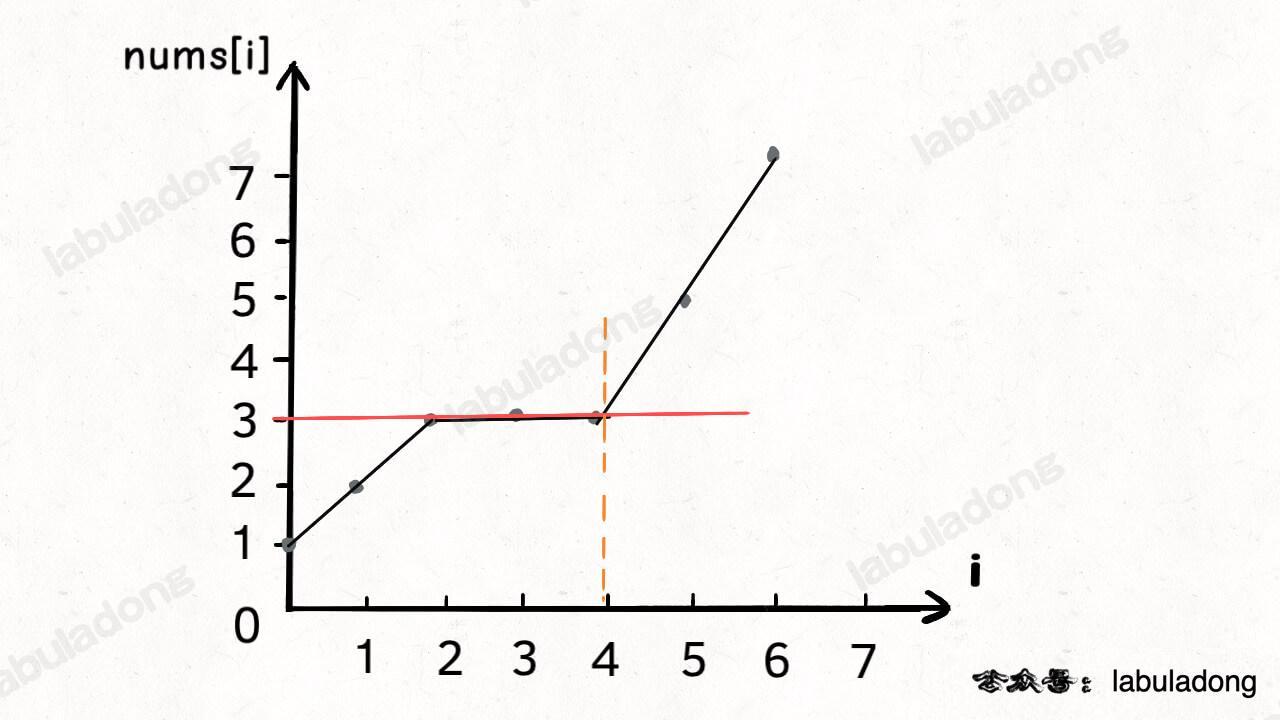
输入同上，那么算法就会返回索引 4，如果画一个图，就是这样：

好，上述内容都属于复习，我想读到这里的读者应该都能理解。记住上述的图像，所有能够抽象出上述图像的问题，都可以使用二分搜索解决。

🌟

#二分搜索问题的泛化

什么问题可以运用二分搜索算法技巧？

首先，你要从题目中抽象出一个自变量 x，一个关于 x 的函数 f(x)，以及一个目标值 target。

同时，x, f(x), target 还要满足以下条件：

1、f(x) 必须是在 x 上的单调函数（单调增单调减都可以）。

2、题目是让你计算满足约束条件 f(x) == target 时的 x 的值。

上述规则听起来有点抽象，来举个具体的例子：

给你一个升序排列的有序数组 nums 以及一个目标元素 target，请你计算 target 在数组中的索引位置，如果有多个目标元素，返回最小的索引。

这就是「搜索左侧边界」这个基本题型，解法代码之前都写了，但这里面 x, f(x), target 分别是什么呢？

我们可以把数组中元素的索引认为是自变量 x，函数关系 f(x) 就可以这样设定：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

// 函数 f(x) 是关于自变量 x 的单调递增函数
// 入参 nums 是不会改变的，所以可以忽略，不算自变量
int f(int x, int[] nums) {
    return nums[x];
}

其实这个函数 f 就是在访问数组 nums，因为题目给我们的数组 nums 是升序排列的，所以函数 f(x) 就是在 x 上单调递增的函数。

最后，题目让我们求什么来着？是不是让我们计算元素 target 的最左侧索引？

是不是就相当于在问我们「满足 f(x) == target 的 x 的最小值是多少」？

画个图，如下：

如果遇到一个算法问题，能够把它抽象成这幅图，就可以对它运用二分搜索算法。

算法代码如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

// 函数 f 是关于自变量 x 的单调递增函数
int f(int x, int[] nums) {
    return nums[x];
}

int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(mid, nums) == target) {
            // 当找到 target 时，收缩右侧边界
            right = mid;
        } else if (f(mid, nums) < target) {
            left = mid + 1;
        } else if (f(mid, nums) > target) {
            right = mid;
        }
    }
    return left;
}

这段代码把之前的代码微调了一下，把直接访问 nums[mid] 套了一层函数 f，其实就是多此一举，但是，这样能抽象出二分搜索思想在具体算法问题中的框架。

#运用二分搜索的套路框架

想要运用二分搜索解决具体的算法问题，可以从以下代码框架着手思考：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

// 函数 f 是关于自变量 x 的单调函数
int f(int x) {
    // ...
}

// 主函数，在 f(x) == target 的约束下求 x 的最值
int solution(int[] nums, int target) {
    if (nums.length == 0) return -1;
    // 问自己：自变量 x 的最小值是多少？
    int left = ...;
    // 问自己：自变量 x 的最大值是多少？
    int right = ... + 1;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(mid) == target) {
            // 问自己：题目是求左边界还是右边界？
            // ...
        } else if (f(mid) < target) {
            // 问自己：怎么让 f(x) 大一点？
            // ...
        } else if (f(mid) > target) {
            // 问自己：怎么让 f(x) 小一点？
            // ...
        }
    }
    return left;
}

具体来说，想要用二分搜索算法解决问题，分为以下几步：

1、确定 x, f(x), target 分别是什么，并写出函数 f 的代码。

2、找到 x 的取值范围作为二分搜索的搜索区间，初始化 left 和 right 变量。

3、根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

下面用几道例题来讲解这个流程。

#例题一、珂珂吃香蕉

这是力扣第 875 题「爱吃香蕉的珂珂open in new window」：

875. 爱吃香蕉的珂珂 | 力扣 | LeetCode |

珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。

珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数）。

示例 1：

输入：piles = [3,6,7,11], h = 8
输出：4

示例 2：

输入：piles = [30,11,23,4,20], h = 5
输出：30

示例 3：

输入：piles = [30,11,23,4,20], h = 6
输出：23

提示：

1 <= piles.length <= 10⁴
piles.length <= h <= 10⁹
1 <= piles[i] <= 10⁹

珂珂每小时最多只能吃一堆香蕉，如果吃不完的话留到下一小时再吃；如果吃完了这一堆还有胃口，也只会等到下一小时才会吃下一堆。

他想在警卫回来之前吃完所有香蕉，让我们确定吃香蕉的最小速度 K。函数签名如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

int minEatingSpeed(int[] piles, int H);

那么，对于这道题，如何运用刚才总结的套路，写出二分搜索解法代码？

按步骤思考即可：

1、确定 x, f(x), target 分别是什么，并写出函数 f 的代码。

自变量 x 是什么呢？回忆之前的函数图像，二分搜索的本质就是在搜索自变量。

所以，题目让求什么，就把什么设为自变量，珂珂吃香蕉的速度就是自变量 x。

那么，在 x 上单调的函数关系 f(x) 是什么？

显然，吃香蕉的速度越快，吃完所有香蕉堆所需的时间就越少，速度和时间就是一个单调函数关系。

所以，f(x) 函数就可以这样定义：

若吃香蕉的速度为 x 根/小时，则需要 f(x) 小时吃完所有香蕉。

代码实现如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

// 定义：速度为 x 时，需要 f(x) 小时吃完所有香蕉
// f(x) 随着 x 的增加单调递减
long f(int[] piles, int x) {
    long hours = 0;
    for (int i = 0; i < piles.length; i++) {
        hours += piles[i] / x;
        if (piles[i] % x > 0) {
            hours++;
        }
    }
    return hours;
}

#例题二、运送货物

再看看力扣第 1011 题「在 D 天内送达包裹的能力open in new window」：

1011. 在 D 天内送达包裹的能力 | 力扣 | LeetCode |

传送带上的包裹必须在 days 天内从一个港口运送到另一个港口。

传送带上的第 i 个包裹的重量为 weights[i]。每一天，我们都会按给出重量（weights）的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。

返回能在 days 天内将传送带上的所有包裹送达的船的最低运载能力。

示例 1：

输入：weights = [1,2,3,4,5,6,7,8,9,10], days = 5
输出：15
解释：
船舶最低载重 15 就能够在 5 天内送达所有包裹，如下所示：
第 1 天：1, 2, 3, 4, 5
第 2 天：6, 7
第 3 天：8
第 4 天：9
第 5 天：10
请注意，货物必须按照给定的顺序装运，因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。

示例 2：

输入：weights = [3,2,2,4,1,4], days = 3

输出：6

解释：

船舶最低载重 6 就能够在 3 天内送达所有包裹，如下所示：

第 1 天：3, 2

第 2 天：2, 4

第 3 天：1, 4

示例 3：

输入：weights = [1,2,3,1,1], days = 4

输出：3

解释：

第 1 天：1

第 2 天：2

第 3 天：3

第 4 天：1, 1

提示：

1 <= days <= weights.length <= 5 * 10⁴
1 <= weights[i] <= 500

要在 D 天内按顺序运输完所有货物，货物不可分割，如何确定运输的最小载重呢？

函数签名如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

int shipWithinDays(int[] weights, int days);

和上一道题一样的，我们按照流程来就行：

1、确定 x, f(x), target 分别是什么，并写出函数 f 的代码。

题目问什么，什么就是自变量，也就是说船的运载能力就是自变量 x。

运输天数和运载能力成反比，所以可以让 f(x) 计算 x 的运载能力下需要的运输天数，那么 f(x) 是单调递减的。

函数 f(x) 的实现如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

// 定义：当运载能力为 x 时，需要 f(x) 天运完所有货物
// f(x) 随着 x 的增加单调递减
int f(int[] weights, int x) {
    int days = 0;
    for (int i = 0; i < weights.length; ) {
        // 尽可能多装货物
        int cap = x;
        while (i < weights.length) {
            if (cap < weights[i]) break;
            else cap -= weights[i];
            i++;
        }
        days++;
    }
    return days;
}

对于这道题，target 显然就是运输天数 D，我们要在 f(x) == D 的约束下，算出船的最小载重。

2、找到 x 的取值范围作为二分搜索的搜索区间，初始化 left 和 right 变量。

船的最小载重是多少？最大载重是多少？

显然，船的最小载重应该是 weights 数组中元素的最大值，因为每次至少得装一件货物走，不能说装不下嘛。

最大载重显然就是weights 数组所有元素之和，也就是一次把所有货物都装走。

这样就确定了搜索区间 [left, right)：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

public int shipWithinDays(int[] weights, int days) {
    int left = 0;
    // 注意，right 是开区间，所以额外加一
    int right = 1;
    for (int w : weights) {
        left = Math.max(left, w);
        right += w;
    }
    
    // ...
}

3、需要根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

现在我们确定了自变量 x 是船的载重能力，f(x) 是单调递减的函数，target 就是运输总天数限制 D，题目要我们计算船的最小载重，也就是 x 要尽可能小：

这就是搜索左侧边界的二分搜索嘛，结合上图就可写出二分搜索代码：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

public int shipWithinDays(int[] weights, int days) {
    int left = 0;
    // 注意，right 是开区间，所以额外加一
    int right = 1;
    for (int w : weights) {
        left = Math.max(left, w);
        right += w;
    }
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(weights, mid) == days) {
            // 搜索左侧边界，则需要收缩右侧边界
            right = mid;
        } else if (f(weights, mid) < days) {
            // 需要让 f(x) 的返回值大一些
            right = mid;
        } else if (f(weights, mid) > days) {
            // 需要让 f(x) 的返回值小一些
            left = mid + 1;
        }
    }
    
    return left;
}

到这里，这道题的解法也写出来了，我们合并一下多余的 if 分支，提高代码运行速度，最终代码如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

public int shipWithinDays(int[] weights, int days) {
    int left = 0;
    int right = 1;
    for (int w : weights) {
        left = Math.max(left, w);
        right += w;
    }

    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(weights, mid) <= days) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }

    return left;
}

int f(int[] weights, int x) {
    // 见上文
}

🍭 代码可视化动画 🍭

#例题三、分割数组

我们实操一下力扣第 410 题「分割数组的最大值open in new window」，难度为困难：

410. 分割数组的最大值 | 力扣 | LeetCode |

给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

设计一个算法使得这 m 个子数组各自和的最大值最小。

示例 1：

输入：nums = [7,2,5,10,8], m = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。 
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

示例 2：

输入：nums = [1,2,3,4,5], m = 2
输出：9

示例 3：

输入：nums = [1,4,4], m = 3
输出：4

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 10⁶
1 <= m <= min(50, nums.length)

函数签名如下：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

int splitArray(int[] nums, int m);

这个题目有点类似前文一道经典动态规划题目高楼扔鸡蛋，题目比较绕，又是最大值又是最小值的。

简单说，给你输入一个数组 nums 和数字 m，你要把 nums 分割成 m 个子数组。

肯定有不止一种分割方法，每种分割方法都会把 nums 分成 m 个子数组，这 m 个子数组中肯定有一个和最大的子数组对吧。

我们想要找一个分割方法，该方法分割出的最大子数组和是所有方法中最大子数组和最小的。

请你的算法返回这个分割方法对应的最大子数组和。

我滴妈呀，这个题目看了就觉得难的不行，完全没思路，这题怎么运用我们之前说套路，转化成二分搜索呢？

其实，这道题和上面讲的运输问题是一模一样的，不相信的话我给你改写一下题目：

你只有一艘货船，现在有若干货物，每个货物的重量是 nums[i]，现在你需要在 m 天内将这些货物运走，请问你的货船的最小载重是多少？

这不就是刚才我们解决的力扣第 1011 题「在 D 天内送达包裹的能力open in new window」吗？

货船每天运走的货物就是 nums 的一个子数组；在 m 天内运完就是将 nums 划分成 m 个子数组；让货船的载重尽可能小，就是让所有子数组中最大的那个子数组元素之和尽可能小。

所以这道题的解法直接复制粘贴运输问题的解法代码即可：

java 🟢cpp 🤖python 🤖go 🤖javascript 🤖

int splitArray(int[] nums, int m) {
    return shipWithinDays(nums, m);
}

int shipWithinDays(int[] weights, int days) {
    // 见上文
}

int f(int[] weights, int x) {
    // 见上文
}